세상에서 가장 쉬운 베이즈 통계학 입문

우선, 피부에 와 닿는 몬티홀 문제부터 말해볼까요? 널리 알려져 있는 문제입니다.

 

커튼으로 가려진 문 A,B,C 세 개가 있습니다. 이 중 한 커튼 뒤에 경품으로 자동차가 있습니다. 경품이 있는 문을 맞추면 당첨, 차는 당신 것입니다.
자, 당신은 A를 골랐습니다. 그런데 갑자기 사회자가 커튼 B를 열어서 그 뒤에 아무것도 없음을 보입니다. 이제 당신은 그대로 A를 유지할까요, C로 바꿔야할까요?

정답: 당신은 C로 바꿔야 유리합니다.

매우 유명한 문제이고, 확률에 대해 인간의 이성과 추론이 얼마나 오작동하기 쉬운지 알려주는 문제입니다.

좀 더 미묘한 사례를 들어볼까요?

A라는 병에 걸릴 확률은 0.1%입니다.
이 병에 걸렸는지 간이검사를 할 경우, 실제 병이 있다면 95% 확률로 양성이 나옵니다. 단, 간이진단이기 때문에 건강한 사람이 양성이라고 오진될 확률은 2%가 있습니다.
자, 당신은 이 검사를 받았고 양성이 나왔습니다. 실제로 이 병일 확률은 얼마나 될까요?

답: 4.5%입니다.

존 브록만의 책을 읽다가, '현대에 꼭 알아야될 단 하나의 수학이 있다면 그건 베이즈 통계학'이란 문장을 읽었습니다. 그렇지 않아도 베이지안에 대해선 갈증이 많던 차라 책을 찾아 봤습니다. 목적에 맞는 책을 찾은것 같습니다.

 

먼저 베이지안에 대해 제가 아는 두 가지 다른 세상에서 시작하는게 쉽겠네요.

하나는 수식으로서의 베이지안입니다. 베이지안은 흔히 말하는 조건부 확률입니다.

P(A|B) = P(A ∩ B)/P(B)

로 흔히 표시됩니다. B 상황일 때 A가 일어날 확률입니다. 학교 시험 문제에선 우산을 가지고 나갔을 때 비가 올 확률 어쩌고하는 문제가 대표적입니다. 저는 공식을 풀어서 답은 맞췄지만 이걸 배워 어따 써먹나 항상 궁금했습니다

 

둘째로, 철학으로서의 베이지안입니다. 불확실한 세상을 기술하는 방법. 모든 걸 알지 못하는 상항에서 단서가 추가 될수록 실체에 가까이 가는 수학적 방법입니다. 이쯤되면 연금술의 광고문구 같습니다. 심지어 이 책의 저자도 베이즈 통계학은 '수상하고 미심쩍은' 부분이 많다'고 자인합니다.

 

이유는 사전확률 때문입니다. 베이즈 방법에선 어떤 상황에 대한 사전확률을 상정합니다. 그리고 관측된 결과를 이용해사후확률을 갱신하는게 베이지안의 핵심입니다. 심지어 이 사전확률은 주관적이어도 무방합니다. (다만 실체에 보다 빠르게 접근하려면 합리적인 추정이 더 유리할 뿐입니다.)

 

실제로 구글 같은 실시간 검색이나, 스팸 필터에서 베이지안은 필수 요소이기도 합니다.

 

이 책의 매력은 적분, 정규분포 같은 사람 기죽이는 수식을 하나도 쓰지 않고 베이지안을 설명한다는 점입니다. 면적을 이용해 이야기를 전개하므로 매우 직관적이면서도 원본의 손실없이 핵심을 정확히 전달합니다.

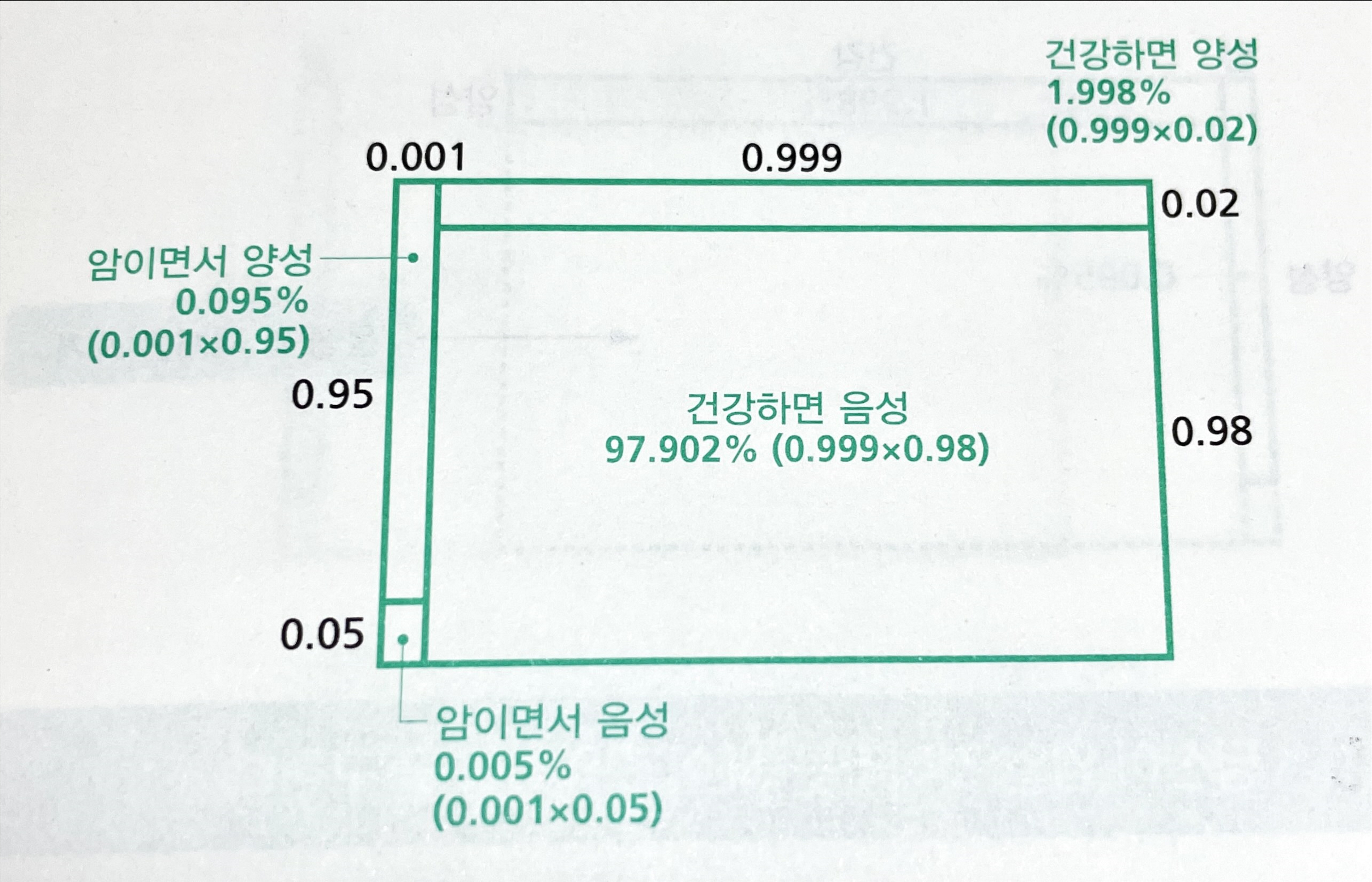
예컨대 서두 중 둘째 문제는 이렇게 표현됩니다. 제대로 진단할 확률이 95%나 되는데도 양성진단 나왔을 때 실제 병일 확률이 4.5%라는 반직관적인 이야기는, 모수에 대한 이해가 우리 뇌에 프로그램되어 있지 않기 때문입니다. 그림에서 보듯, 이미 천명중 999명의 확률로 환자가 아니란게 중요합니다. 이제 양성 진단을 받아 0.1%에서 4.5%로 45배나 위험해졌지만, 아직 천명에 5명 정도 확률입니다. 이제 추가의 진단을 받아보면 더 자세히 알 수 있겠죠.

 

책은 단계를 높여가며 베이즈 통계학의 기본을 차근차근 설명합니다. 그러면서도 기존 네이만-피어슨 통계학과 상통함을 다양한 각도로 보여줍니다. 책의 후반부는 좀 더 온전한 이해를 위해 적분식과 정규분포, 베타분포를 고육지책으로 씁니다만, 이책의 백미는 딱 앞의 절반입니다. 면적과 산수만으로도 베이즈 통계학의 진수를 맛볼 수 있습니다.

 

Inuit Points ★★★★☆

시험에선 조건부 확률 문제를 잘 풀었지만, 실생활에서 단 한번도 적용해 본 적이 없습니다. 이번에야 비로소 베이지안이 어떤 의미인지 제대로 알았습니다. 덤으로 몬티홀 문제에서 제가 혼란에 빠진 이유도 알았습니다. C 커튼 뒤에 차가 있을 확률이 그대로 1/2인지, 2/3로 올라가는지는 사회자의 행동에 달려 있음을 책에서 짚어둡니다. 즉 사회자가 재미를 위해 차가 없는 커튼을 열어 제낀다면 추가의 정보를 넣었기 때문에 확률이 갱신됩니다. 만일 사회자가 랜덤하게 연다면 직관처럼 느껴지는 원래 확률 그대로입니다.

 

감히 주관을 말하고 불완전성을 용인하는 태도 때문에, 주류 통계학인 네이만-피어슨 통계학으로부터 핍박과 멸시까지 받던 베이지안입니다. 저는 책에서 두 진영이 결국 등가라는 증명을 할때 이런 생각이 들었습니다.

네이만-피어슨이 뉴튼 역학이면, 베이지안은 양자역학이구나.

별 넷 기쁘게 줍니다.